今回のお話は、「順列」と「組み合わせ」です。 順列とは「並べる」こと。 組み合わせとは、読んで字の如く「組み合わせる」ことです。 やはり、この違いを根本からしっかりと理解をしておくことは場合の数の学習においては非常に重要です。
場合の数 順列 組み合わせ-ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。組合せとは いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています. 順列 $\rightarrow$ 順序を考慮 (区別)する.
場合の数 順列 組み合わせのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「場合の数 順列 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 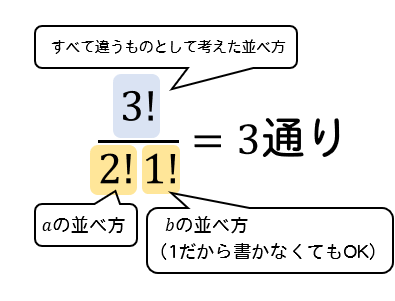 |
場合の数の組み合わせのまとめです。「同じものを含む順列」もここであつかいます。 必要な準備 和の法則と積の法則 あうるさん 組み合わせも公式を理解するのに和の法則と積の法則をつTwitterも不定期に更新中 ⇒シータ @高校数学マストラ 数学が苦手な方は「Step1:基礎知識を高速インプットし
Incoming Term: 場合の数 順列 組み合わせ, 場合の数 順列 組み合わせ 算数,




0 件のコメント:
コメントを投稿