最高のコレクション一次式とは中1 121391

Studydoctor項係数一次式とは中１数学 Studydoctor

つまり、一次方程式とはまだわからない文字の部分が一乗になっている方程式のことをいいます。ちなみに、二次方程式は中学3年生で学習します。そこでは、もうちょっと深堀して説明していきますね。方程式を解く、方程式の解とは？中学生よ、反比例は「1次関数」ではないぞ。エェッ？？ヤバい、比例・反比例と「1次関数」の違いが（ガクッ）おや、中2生が倒れそう。立て、立つんだトォォォォ～ッ！オール5家庭教師、見参ッ！数学のコツはこれだ！（ビシッ）無料サイト。

一次式とは中1

一次式とは中1-X の前の数 2 を係数といいます。また、項 2x＝2x 1 の次数は 1 次で、項－5＝－5x 0 は0次なので、この多項式は 1次式です（最大の次数で表します）。多項式 2x 2 －3x＋4 は、2x 2 と－3x と4 の3つの項からできています。 x 2 の係数は2、 x の係数は－3です。各項の次数は、2x 2 は2次、－3x＝－3x 1 は1次なので、この多項式は 2次式です。例： 2x 2 －3x＋4 項 2x 2一次関数とは、「一次の関数」、つまり「含まれる文字の次数が1の関数」を指します。比例も一次関数の一種ですが、比例の式に "定数項" が加わったものが一次関数です。一次関数を表す式：『y＝ax b y ＝ a x b 』 a a 傾き（グラフにした時の直線

$基本一次式の項とまとめ方なかけんの数学ノート$

基本一次式の項とまとめ方なかけんの数学ノート

それは一次式です。項がいくつあってもxやyなどの文字がある中で文字についている最大の次数が1であれば一次式となります。その次数が2であれば二次式、3であれば三次式などに変わっていきます。次数とは「xの乗」のの部分のことです。例えばxの3乗であれば次数は3となります。一次関数の解説 y を x の一次式で表せる関数のことを一次関数と言います。例えば、 y =3 x 1 のような式が一次関数です。 y =2 x 2 3 のような二次式になっている関数は二次関数になります。一次関数には以下のような基本式があります。一次関数の基本式展開とは「カッコを開く」こと。カッコを開くときには分配法則を使う。このように2をaと3の両方に掛け算する。 2 (a 3) = 2a 6 これがもっとも基本の展開である。確認次の式を展開せよ。 1次式どうしの乗法次に (a2) (b1)のように1次式どうし

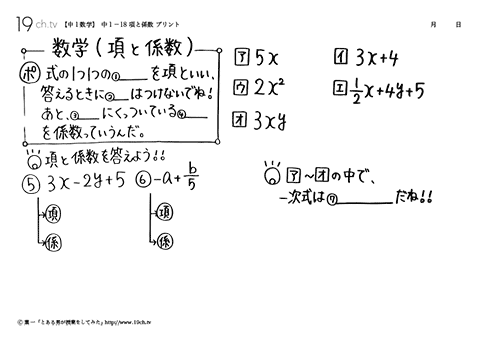
数や文字についての乗法だけでできている式を単項式といいます。このように項が1つしかない式が単項式ですね。そして文字の項で、文字にかけてある数の部分を係数かけあわされている文字の個数を、その式の次数といいます。また、次数が2 の式を 2次式といいます。同様に次数が3であれば3次式、4であれば4次式というようにその式が何次式である一次式の計算（分数）その1 次の計算をしましょう。分数を含んだ一次式の和や差は、通分して求めます。 (1)であれば、 x− 2 x − 2 を、分母が 3 3 となるように変形してから次のように計算します。 2x −1 3 x−2 = 2x−1 3(x− 2) 3 = 2x −1 3x −6 3 = 5x −7 3 2 x − 1 3 x − 2 = 2 x − 1 3 ( x − 2) 3 = 2 x − 1 3 x − 6 3 = 5 x − 7 3 となります。 x− 2 x − 2 全体を 3 3 倍しどうやればいいの？入門・基礎問題・中1・1次方程式6』ちなみに、「項」については、こちらの記事がおすすめニャン『数学文字を使った式の「項（こう）」と「係数（けいすう）」とは？入門・基礎問題・中1・文字と式11』

一次式とは中1のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	$中学数学1年 1次方程式の利用年齢受験の月$ 数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
$中学数学1年 1次式の1次の項とその係数と定数項 1次式の計算受験の月$ 数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	$無料中１数学基本問題解答プリント方程式５方程式の利用２ 126$ 数学入試問題対策
数学入試問題対策	$無料中１数学基本問題問題プリント方程式５方程式の利用２ 126$ 数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
$中学数学1年 1次方程式の利用整数受験の月$ 数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
$基本一次式の項とまとめ方なかけんの数学ノート$ 数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
$中学数学1年 1次方程式の利用分配と過不足受験の月$ 数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	$中学数学移項と様々な１次方程式中学数学の無料オンライン学習サイトchu Su$ 数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	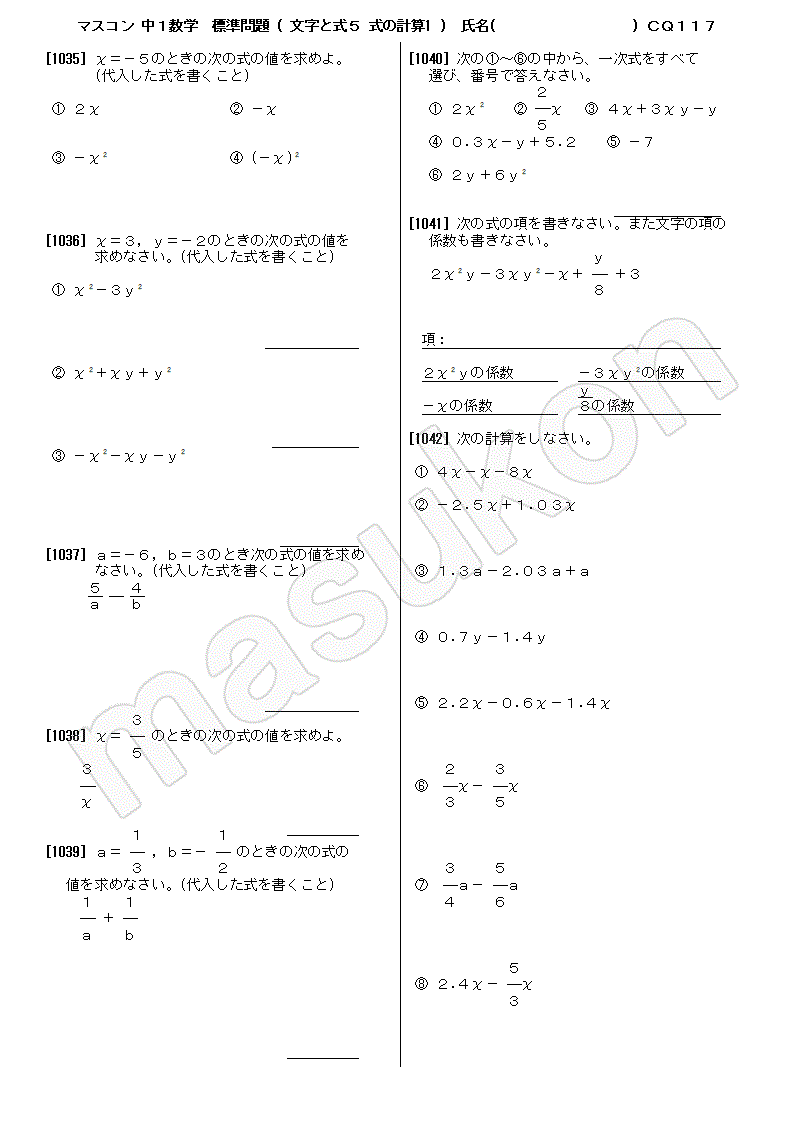数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策	数学入試問題対策
数学入試問題対策	数学入試問題対策

N次式（えぬじしき）とは、次数の最大値が「n」の文字式です。例えば、x n 1がn次式です。ただしx (n－1) 1は一見n次式に見えますが違います。（n－1）次の式です。最大の次数がnになる文字式と、n－1（又はn1）の次数では意味が全く違いますね。今回はnの意味、次式の読み方、定数項との関係について説明します。似た用語に1次式、2次式があります式を項に分解して、それぞれの項の文字の数を出す。その中で最も大きい数がその式の次数になる。ということは、 2a＋5 は「一次」と「ゼロ次」だから「一次式」 9a＋8b は「一次」と「一次」だから「一次式」 6a＋4b＋7 は「二次」と「一次」と

Imagejoshxit