正方形の一辺の長さは abとなるから、これは与 えられた長さa, bからabを作図する問題に帰着 できる。図3の長方形ABCDにおいて、AB=a, BC=bとする。ADの延長上にED=DCとなる点E をとり、AEの中点をMとする。CDの延長上に PM=MAとなる点Pをとる。このとき、直角三角形正八角形 正八角形においては、一つの外角と中心角は45 °で、内角は135°になる。 一辺の長さを a とすれば、周長は 8a 、面積 A は下記となる。 = = () (/) を有理数と平方根で表すことが可能である。= = = = 正八角形の作図 これが正八角形の1辺の長さです。 従って,a+√2a+a=2a+√2a=1700となり, a=1700/(2+√2) 有理化して a=1700(2-√2)/2 =850(2-√2) 以上です。 9人 がナイス!
定規とコンパスを使って
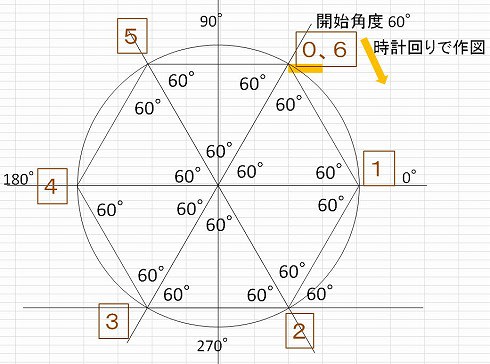
正八角形 一辺の長さ 作図
正八角形 一辺の長さ 作図-め円をもとに, 8つの辺の長さや角の大きさが等しい八角形をつくろう。 課円をもとにつくった八角形は,なぜ,8つの辺の長さと角の大きさが等しいのだろうか? 考①直線ABが8本分(八角形の辺8本は等しい) 解している。Euclidea 17 円に内接する正方形の作図 解説 みのまわりの




問題174 立方体に潜む正多角形
作図 正八角形においては、一つの外角と中心角は45 °で、内角は135°になる。一辺の長さを a とすれば、周長は 8a 、面積 A は下記となる。 = = () 関連事象正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに図 1 図 2 図 3 多角形の外角の 正十角形の作図 正10角形は、正5角形の外接円と、その一辺の二等分線が交わる点を求める方法で作図します。 正十一角形の作図 正11角形。連結式奇数等分器の部分を5枚使います。十文字の照準線の長い部分を重ねる方
八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;正 n 角形の面積は一辺を a とすると n a 2 4 cot π n {\displaystyle {na^{2} \over 4}\cot {\pi \over {n}}} と求められる。 この式は、正 n 角形の外心から、各頂点に向けて、線分を引き、 n 個の二等辺三角形に分割することで容易に証明できる。まず正五角形の一辺と対角線の長さを使う場合です。 一辺を赤色、対角線を青色で表しています。 3通りの大きさが書けることがわかります。 正五角形の作図(第2法) 次に正五角形の一辺と外接円の半径を使う場合です。 一辺を赤色、外接円の半径を緑色
正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の正五角形を(定規とコンパスのみを使って)作図する方法を解説します。 正五角形の作図の原理を理解するために,まずは1辺が1の正五角形の対角線の長さについて考えます。 とにかく作図方法だけ知りたい! という方はページ下部のグレー背景部分(2第47問 正方形と正八角形 図形ドリル 6年生 正八角形 正方形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。



サッカーボールの型紙 エクセルvbaで正六角形を作図しますpart 2 日だまりのエクセルと蝉しぐれ




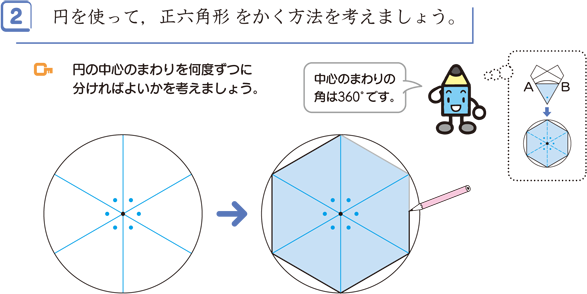
5年算数 円と正多角形 2 わかる教え方のポイント
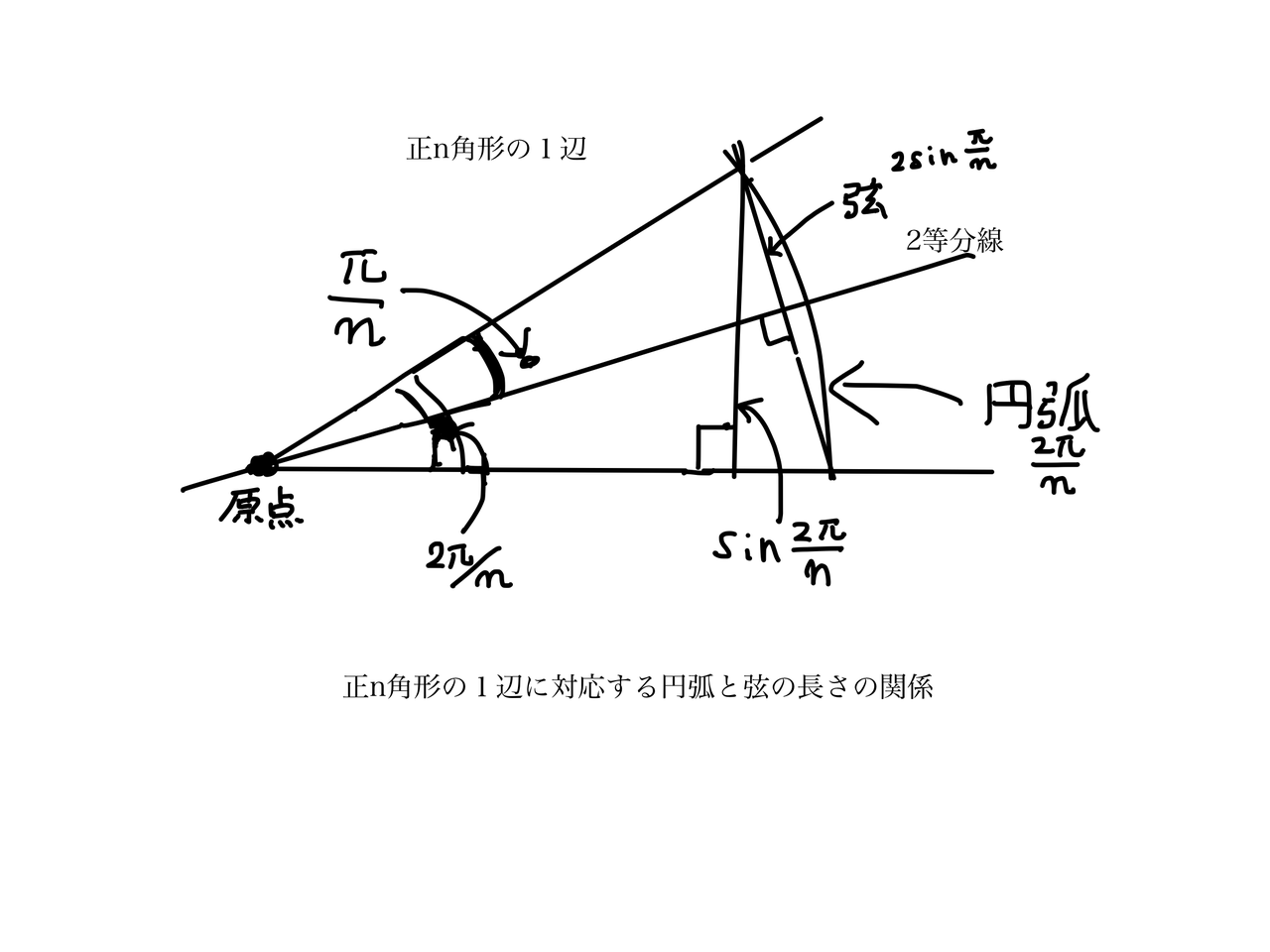
上の解説をそのまま生かして、一辺の長さをaとして aで面積を求めてみます。 見通し 基本的には、上の解説の通りですが、Rをaで表す事ができればよいわけです。 R=h+χ という性質を利用すれば解決できそうです。 解説三角関数使って表記すれば半径1の円に内接する正N角形の一辺の長さは \2\sin(\pi/N)\ なんですが、この値は具体的に加減乗除と累乗根を使って表すことができます。 それを計算してみようという試み。 正三角形 \2\sin(\pi/3) = \sqrt{3}\ 作図クイズアプリ、Euclidea。(5) 辺ADは円周を7等分する基準長さとなるので,円周を7等分できる。 (6) 正7角形を作図する。 付図31 正7角形の作図 補足同様の作図法で,直径ABをn等分すれば,正n角形を作図できる。付図32は正9角形及び正5角形を作図した例である。




Vers Le Haut 正12角形 書き方 正12角形 書き方




Wikizero 五角形
正五角形・正六角形の辺の長さや角の大きさは,どうなっているの 無断複製・転載・翻訳を禁ず GAKKEN B TitleMixi簡単な数学 八角形の公式 八角形の対辺の距離が出せるようにエクセルに式を入れようとしましたが、どうやったらいいのかわかりません。 公式とかってあるんですか? 一辺の長さに2414を掛けると一応の数値はでますが理屈がわかりません13年06月19日 (水) 三角関数使って表記すれば半径1の円に内接する正N角形の一辺の長さは 2sin(π / N) なんですが、この値は具体的に加減乗除と累乗根を使って表すことができます。 それを計算してみようという試み。



定規とコンパスを使って




正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム
正六角形の中に、同じ辺の長さの正三角形が6つ有るので、正三角形の面積が分かれば、その6倍が正六角形の面積となります。 以下が、正三角形の面積を計算する公式です。 正三角形の面積を6倍します。 この式をまとめると以下のようになります。「定規とコンパスで作図」目次 手書きで、正八角形を描く方法を紹介します。 直線定規とコンパスを使う作図方法を2つ。 三角定規の角度や分度器や直線定規の数字を使う描き方は特に解説しません。 正八角形の条件 ・8辺の長さが等しい多角形。 一辺の長さを100にしますので、キーボードから「100」と入力し「Enter」または「Space」で実行をします。 ⑥一辺100の正五角形が完成しました。 参考記事 ・作図補助機能(直交モード・ダイナミック入力)AutoCAD作図の基本 目次へ戻る 4.まとめ
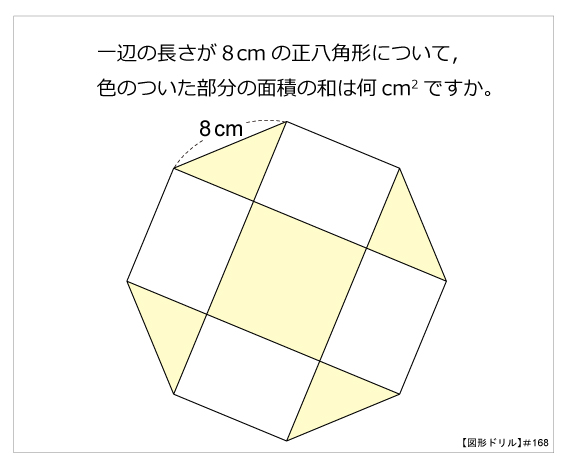



図形ドリル 第168問 正八角形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦




Octagon 八角形 Wikipe Wiki
基本の作図 垂線 正三角形 直線l上の点Aに垂線をたてる A l 点Aにコンパスの針をさし、直線lと2点で交わるように弧を描く コンパス1 2つの交点それぞれに針をさし、弧を描いて交点をつくる (このときのコンパスの幅はコンパス1より広くとり、コンパス2と3で異なってはいけない)垂線の作図を \(2\) 回続けて行えばよいということです。 垂線の作図方法はここでは再確認はしません。 ひし形を作図する 平行線の作図は、まったく別の手順も可能です。 作図の基本であるひし形は、向かいあう辺が平行になっています。思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 解けた方はお気軽に@sansu_seijin宛につぶやい



Wikizero 二十角形



正多角形 算数用語集
ここでは、半径1の円に内接する正五角形の一辺の長さを計算して、正五角形の作図方法を説明します。 正五角形の内角は 2π/5 2 π / 5 ラジアン(72°)であることから、 まず最初に a=cos(2π/5) a = cos ( 2 π / 5) を使って一辺の長さを計算します。 右の図に円に内接する正多角形 万華鏡の筒に内接する正多角形の一辺を計算で求めたかった。 しかし、角数が増えて計算が大変になってきたので、頼りました。 後から星形をカッターで切り抜いた。 大きさは色々でも、形が揃う為。 円を近似するのに何角形一辺3センチの正五角形を例に説明します。 ① Excelを立ち上げ、セルA1に半角の数字3(辺の長さ)を入れてください。 ② セルB1には =2*SIN(RADIANS(180/5)) をコピペ(コピー&ペースト)で入れます。




図形ドリル 第47問 正方形と正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦
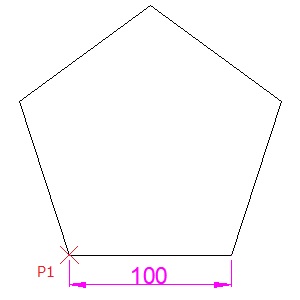



ポリゴンコマンドを使って正多角形を作成 Autocad Cad 製図の無料就職支援講座 Lulucad ルルキャド カレッジ
1辺の長さが与えられた「正六角形」の作図 コンパスを使って、与えられた1辺と等しい長さの辺を描く方法です。 ☆用具:直線定規、コンパス (1) 底辺となる直線abを描く。 (2) コンパスを使い、abの長さと等しい半径の円弧をa、bを中心に描き、円に内接する四角形 Geisya 作図三角形の内接円・外接円のかき方をポイント解説 正多角形の外接円 高精度計算サイト;指定された1辺の長さから、正三角形の面積、周囲の長さ、高さ 正 n 角形の面積は一辺を a とすると に近づいていく。これは、初期の円周率の求め方 で、円周率の歴史上の始まりに位置する。



Www Pref Okayama Jp Uploaded Attachment Pdf




小学5年生 正多角形 算数 Active Learning 学院
6つの三角形の一辺の長さが おなじになるからです。 2/2ページに進む 次のページでは、 円周率の求め方(円の円周と直径の関係) 円周や直径の求め方 を掲載しています。 5年の目次に戻る いっちに算数」の全体目次に戻る5 – エッジ (E)を選択します 作図領域で右クリックします。 ショートカットメニュー が表示されます。 エッジ (E)をクリックします。 一辺の長さを指定できます。 エッジ (E)は、 ポリゴンコマンドのコマンドオプションです。 note補足 一般に正 角形 正五角形の作図 辺が与えられた場合 外接円が与えられた場合 辺の長さが のとき対角線の長さは 半径 の円に内接するとき辺の長さは



定規とコンパスを使って
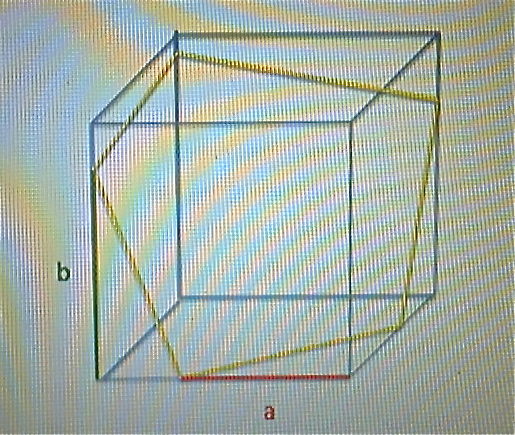



問題174 立方体に潜む正多角形
2 折紙による有理数の作図 一辺の長さが1の正方形の折り紙があるとき,長さ 1 3 はどうやって折れるだろうか? 一般に,0 < x,w ≤ 1とすれば,一辺の長さが1の正方形abcdの辺ab 上に点p を ap = w となるようにとり,辺bc 上に点qをbq = xとなるようにとる.aqとbp直線 ef が正三角形の一辺となる。 直線 eg 、直線 fg も正三角形の一辺。 ② ①と同じ事を行い直線②を引く。 中心点を見つける!! ① 直線(あ)を適当に引く。 点 a 、点 b より同じ長さの曲線①を引く。 中心点からの直線を 二等分する線を見つけること!
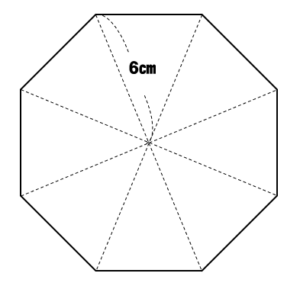



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ




二十角形 Wikipedia




多角形と円5 連問2 正六角形の作図 正3角形の性質を使ってコンパスで作図する方法 Youtube




七角形 Wikiwand




多角形の1辺の長さを指定寸法にあわせる方法 位置合わせ 株式会社後藤商店 Staff Blog




5年算数 円と正多角形 1 わかる教え方



八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋
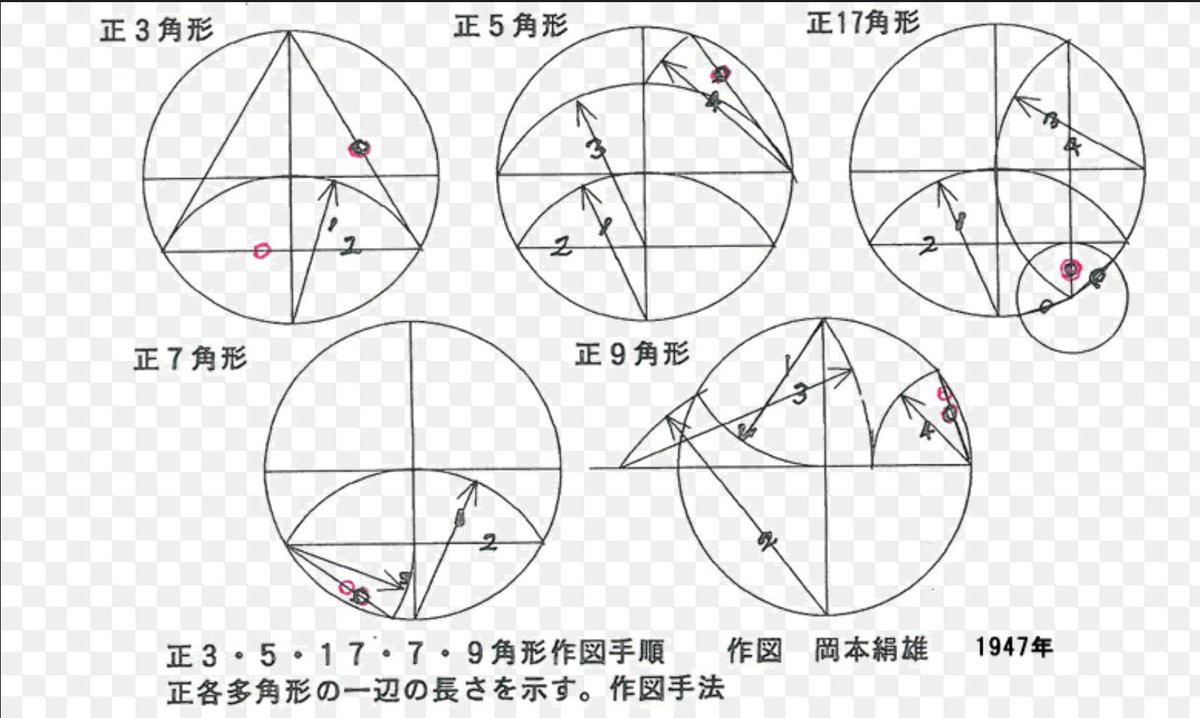



ケンジくん ハリガネの呪い Twitter પર 円に接する正多角形の書き方を使って 円を等分するシートを作りました 中心に空けた穴に円パーツの中心を合わせると均等に分ける線が引けます パイプにも使用可能 対角線を繋げれば任意の大きさの多角形も描けるので




いろいろな正多角形をかいてみよう 家庭学習レシピ




立春過ぎ研修3 正多角形 授業がんばりmath
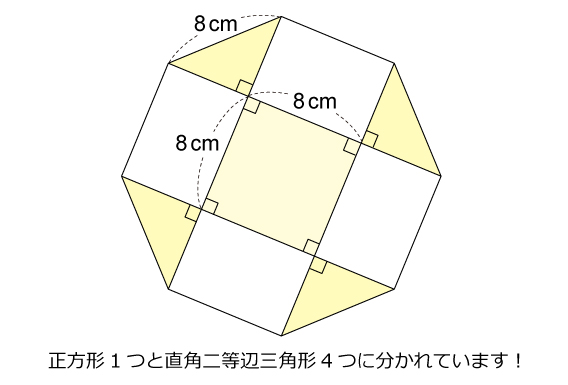



図形ドリル 第168問 正八角形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦




機械設計のための基礎製図



一辺の長さが1の正八角形の面積の簡単な求め方を教えて下さい 答えでは余弦 Yahoo 知恵袋



コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫
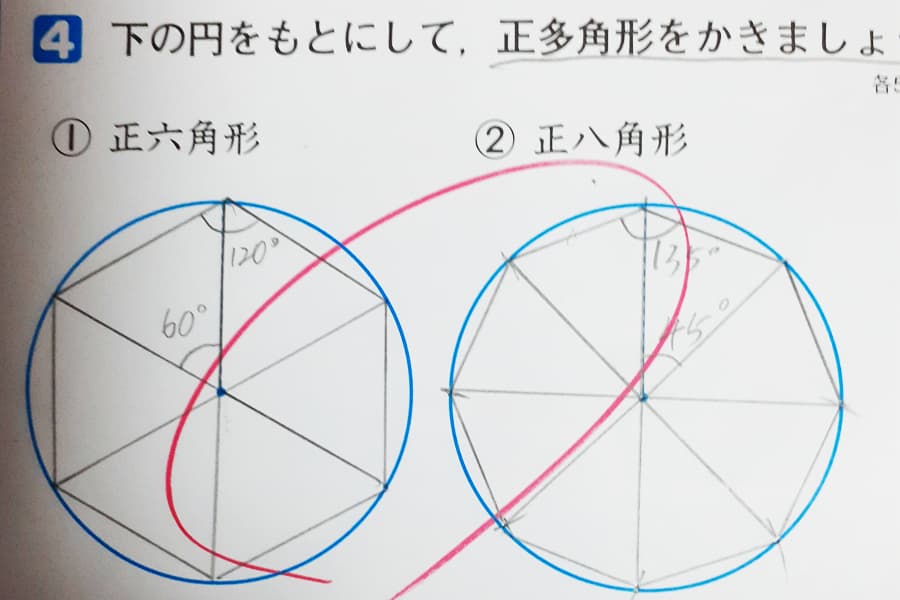



円周率は 3 00 以上であることを証明せよ 受験算数入門




八角形の周囲と面積を計算する方法




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




正八角形の作図 正方形から正八角形の作図の仕方を教えてください 数学 教えて Goo




1辺の長さが4cmの正八角形の面積を求めよ という問題があるの 数学 教えて Goo




八角形 Wikipedia



正六角形角度 平面図形の角度 Lousi Imagine




正9角形の書き方



正多角形2




組合わせをわかりやすく解説 正八角形の各頂点を結び 三角形を作る 高校数学



百聞は一見に如かず 正多角形が自由自在に描ける定規 発明 発想力教育研究所 素数誕生のメカニズム



Happylilac Net Seitakakkei Ans Pdf
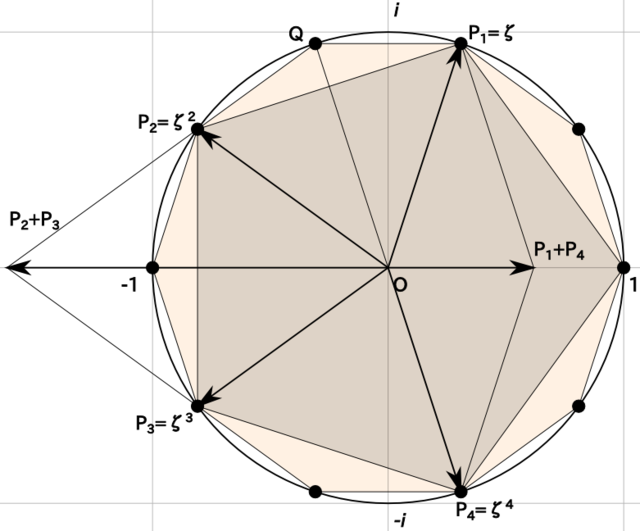



半径1の円に内接する正n角形の一辺の長さ 元祖ワシ的日記




形態の基礎理論 三角形の重心



正七角形の作図 教材作家
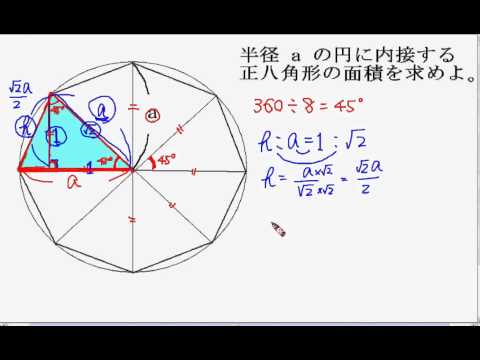



中3数学 正八角形の面積 Youtube



8角形の面積




5年算数 正多角形と円 正八角形をかこう Youtube



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫



1




問題174 立方体に潜む正多角形
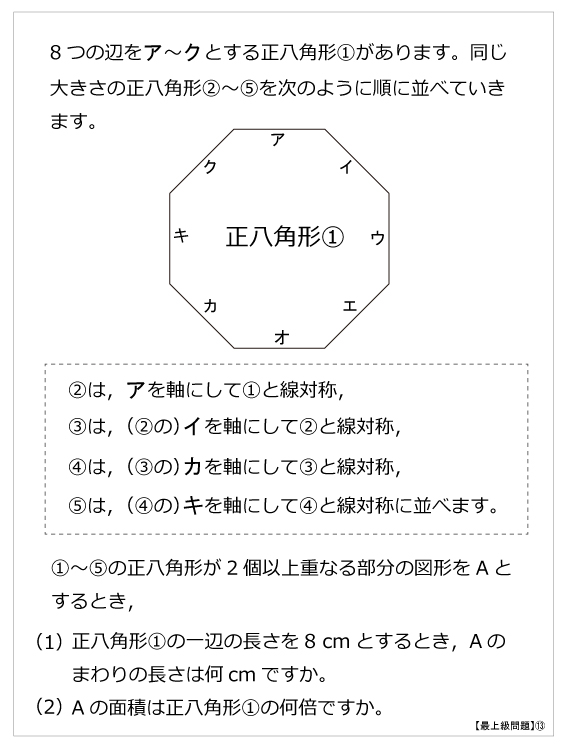



最上級問題 正八角形の問題 算数星人のweb問題集 中学受験算数の問題に挑戦
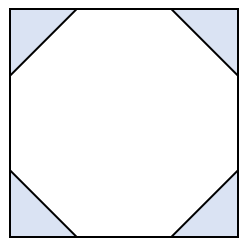



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




Kaizu Blog Excel半径で作図した正多角形の面積計算
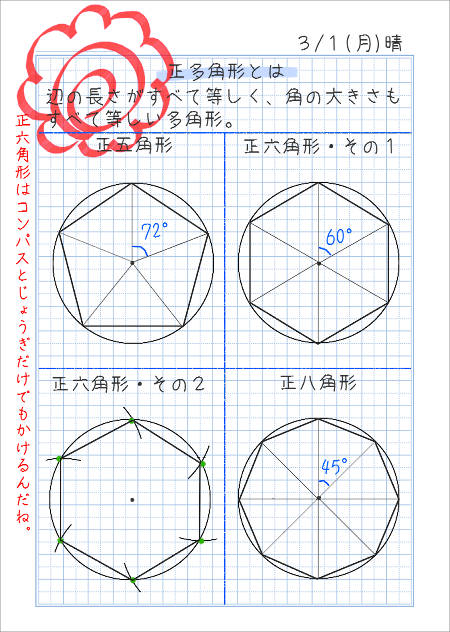



いろいろな正多角形をかいてみよう 家庭学習レシピ



正五角形の作図法 数理女子
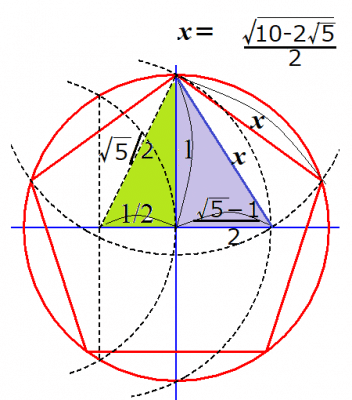



円に内接する正5角形の作図 Sgk Note



コマ大数学科147講 正八面体 ガスコン研究所
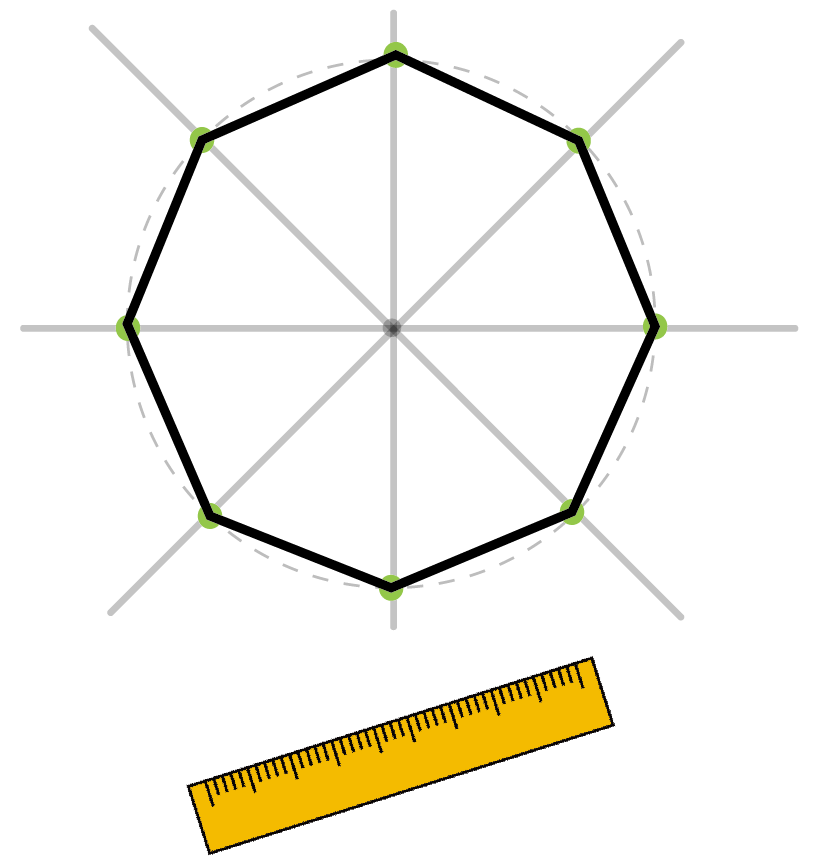



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫




正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




機械設計のための基礎製図



コンパスと定規だけで正七角形を作図できますか Quora
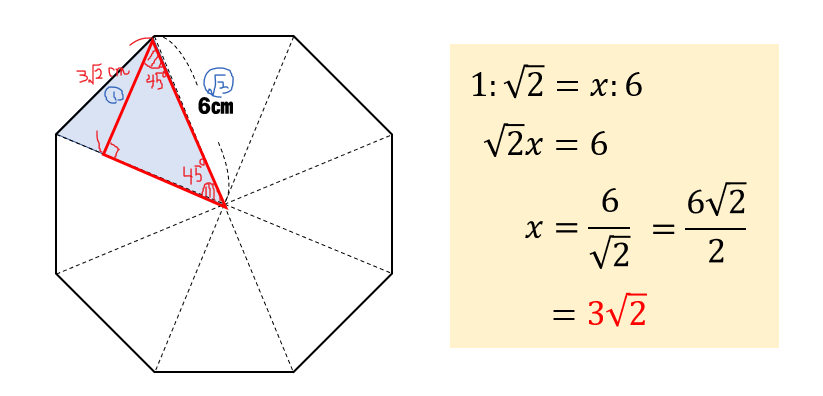



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



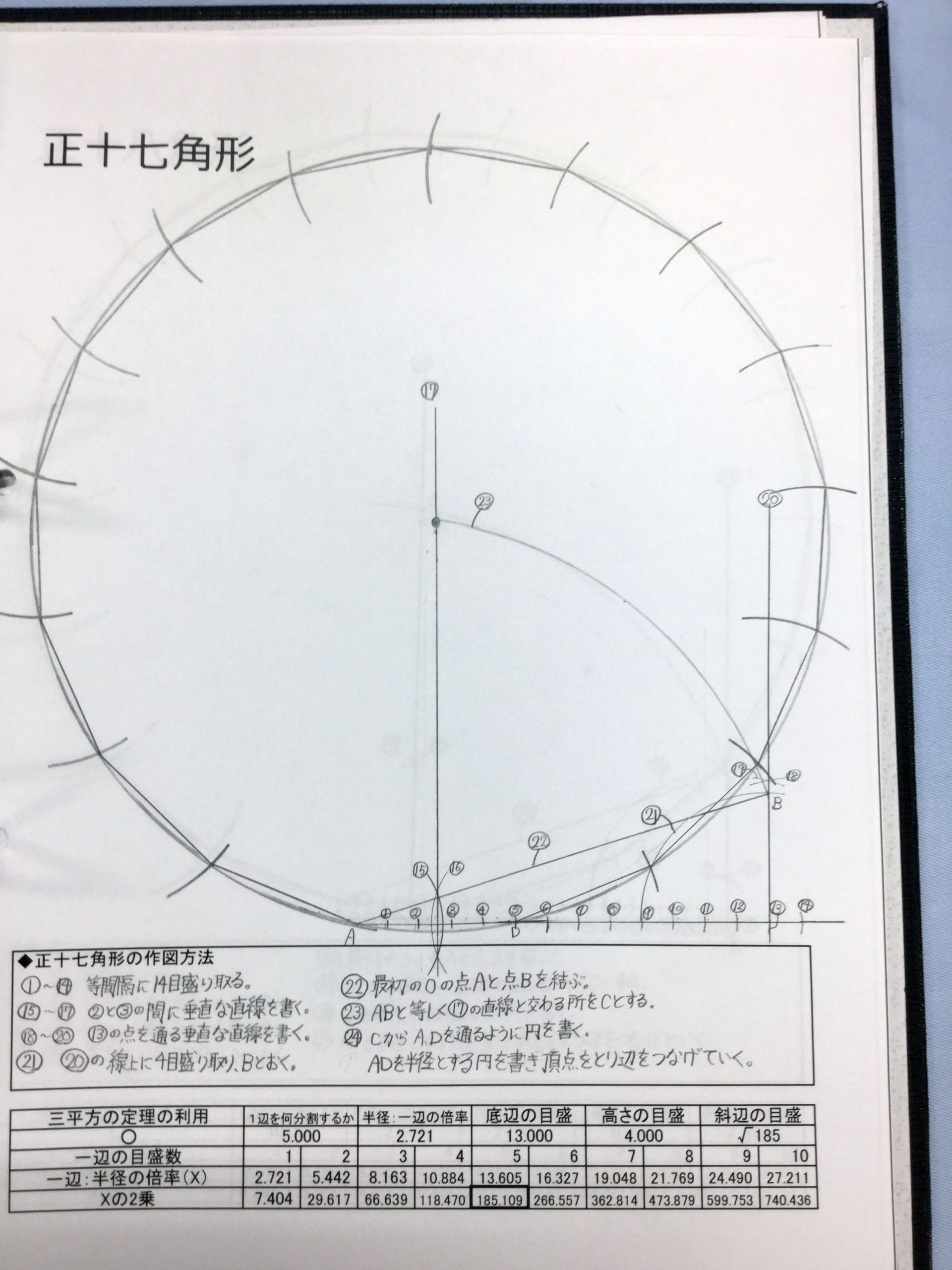
正十七角形の作図
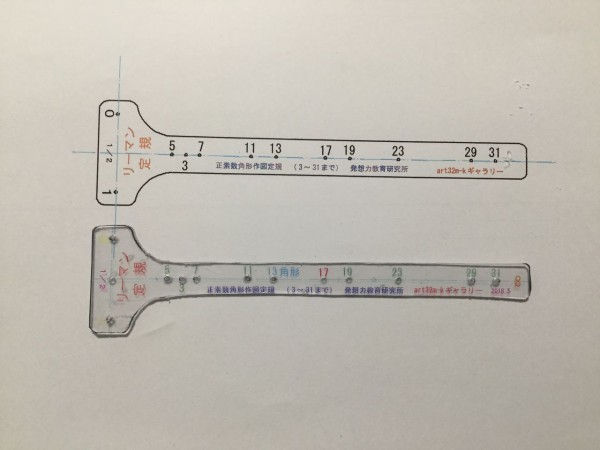



リーマン定規 スケルトン が表すものは 正多角形の真理はピタゴラスの定理 発想力教育研究所 素数誕生のメカニズム



1



正七角形の作図 教材作家



正5角形の作図




八角形 八角形の概要 Weblio辞書
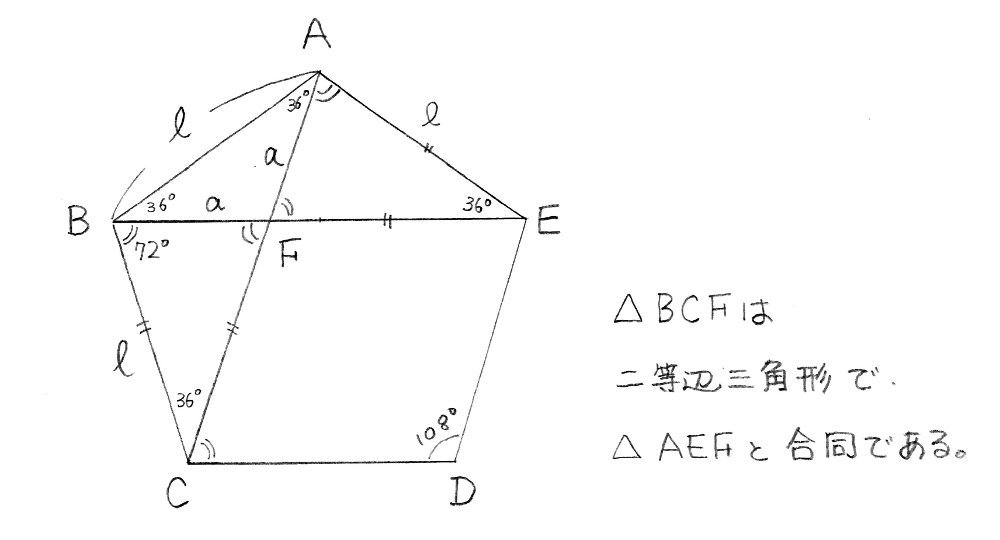



五角形5 辺と対角線の比 Wandering In The Woods



1




正五角形のかき方 小学生の自主学習 分度器 コンパス 定規を使う方法 Youtube
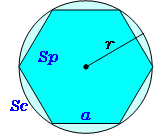



円に内接する正多角形 高精度計算サイト




九角形 Wikipedia



正多角形の描き方



正多角形2
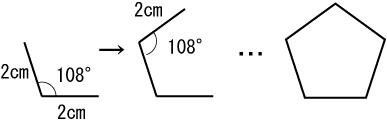



辺の長さが決まった正多角形をかく 5年生 算数の広場



Http Ajgika Ne Jp Gikachiba Shibu Funabashi Daizai Gijyutu1 Pdf




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information



460 x460cmの正四角形の中に正八角形を書いた場合 1辺の長さは何 Yahoo 知恵袋




正多角形 Wikipedia



1
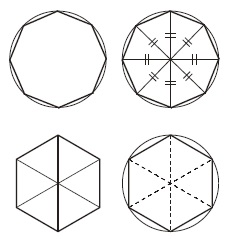



学習指導要領ナビ Jp 小学校 算数 第5学年の内容 b図形 平面図形の性質



Http Www2 Hamajima Co Jp Kyoto Math Pdf Kyomath1808 Pdf



正七角形の作図 教材作家




機械設計のための基礎製図



5年算数 円と正多角形 2 わかる教え方のポイント



正5角形の作図



Http Upload Fku Ed Jp Educ Common Sozaifiledsp Aspx C Id 14 Id 1058 Flid 4868 Set Doc 1




発展 円に内接する正五角形の作図 デザインあ おとなスペシャルで紹介されてたやつ なかけんの数学ノート




八角形の周囲と面積を計算する方法



高校入試数学 正三角形 正六角形 正八角形のテクニックと問題



正多角形と私 慶應義塾普通部




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




高校数学 正多角形の面積の求め方 例題編 映像授業のtry It トライイット



円に内接する正八角形の書き方 合ってますか 円はあらかじめあります Yahoo 知恵袋



角形 E An Design



一辺1の正八角形の対角線の長さを教えてください Aeの長さの出し方を教えてく Yahoo 知恵袋



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫




小学5年生 正多角形 算数 Active Learning 学院



0 件のコメント:
コメントを投稿